Pada pembahasan kali ini kamu akan belajar mengenai gabungan antara materi limit dan fungsi trigonometri yaitu limit fungsi trigonometri. Materi ini membutuhkan pemahaman yang lebih dalam dikarenakan cara penyelesaian soalnya mengikuti aturan limit dan trigonometri.
Pada tulisan ini, kamu akan belajar tentang rumus, teorema yang digunakan, serta pembahasan soal limit trigonometri.
Pengertian Limit Fungsi Trigonometri

Pada pembahasan pertama adalah pengertian dari limit trigonometri. Limit menjelaskan tentang pendekatan nilai terdekat pada suatu fungsi matematika. Pada limit trigonometri, limit digunakan untuk mencari nilai terdekat yang memungkinkan pada suatu fungsi trigonometri. Untuk pengerjaan limit trigonometri menggunakan langkah yang sama dengan pengerjaan limit.
Rumus Limit Fungsi Trigonometri
Untuk menentukan hasil pendekatan limit pada trigonometri, maka digunakan beberapa rumus yaitu rumus dasar dan rumus A mendekati nol seperti di bawah ini.
1. Rumus Dasar Limit Trigonometri
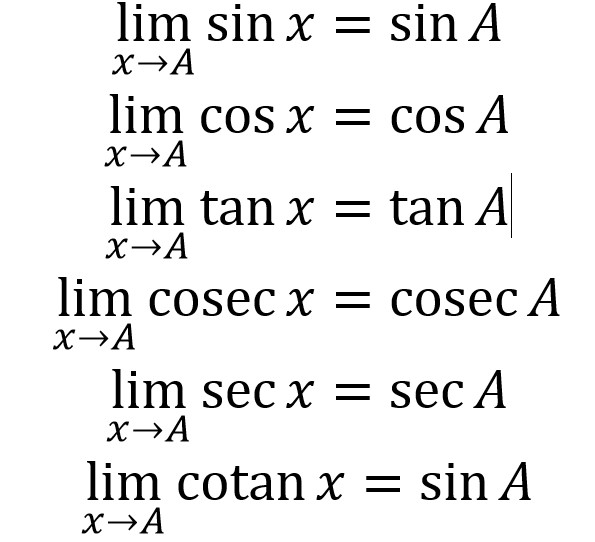
2. Rumus Limit A mendekati nol
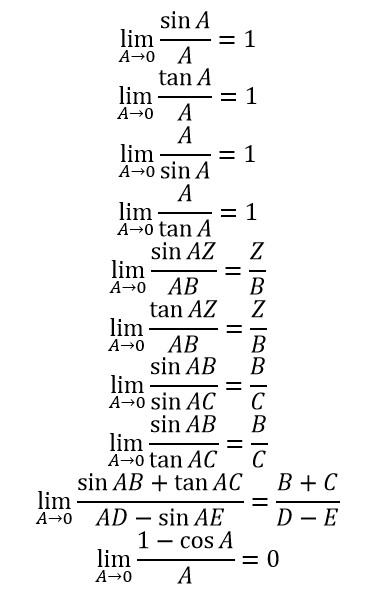
Teorema Limit Fungsi Trigonometri
Dalam limit fungsi trigonometri, terdapat 2 teorema yang berlaku yaitu teorema A dan teorema B.
1. Teorema A![]()
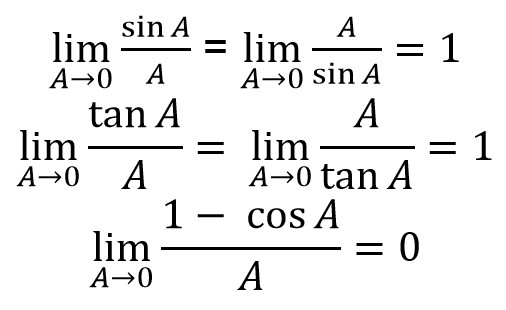
2. Teorema B
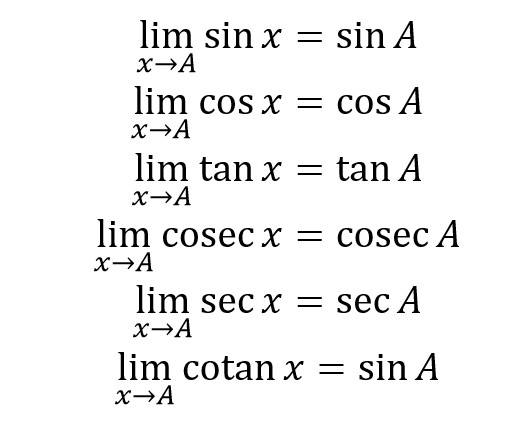
Soal dan Pembahasan Limit Fungsi Trigonometri
1. Diberikan sebuah bentuk limit
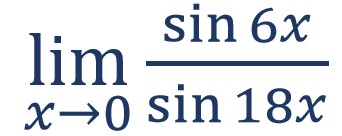
Tentukan hasil dari bentuk limit tersebut…
Untuk mengerjakan soal limit trigonometri, kamu bisa memasukkan nilai x = 0 untuk melihat hasilnya.
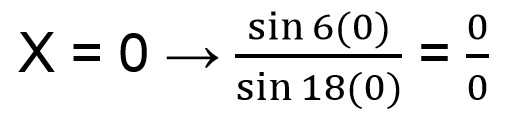
Jika kamu memasukkan nilai x = 0, maka hasilnya menjadi bentuk tak tentu. Sehingga untuk mengerjakan soal di atas, kamu bisa menggunakan rumus limit trigonometeri.

Sehingga kamu bisa langsung menggunakan rumus tersebut dengan nilai B = 6 dan nilai C = 18.
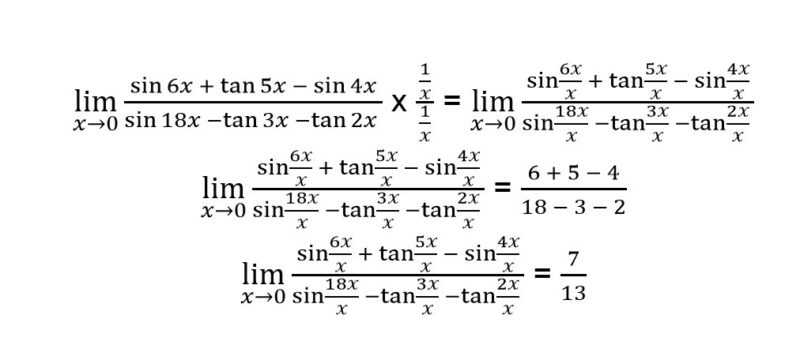
2. Diberikan sebuah bentuk limit
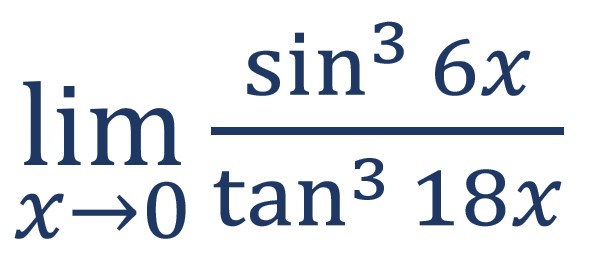
Berapakah hasil dari bentuk limit tersebut…
Untuk mengerjakan soal limit trigonometri, kamu bisa memasukkan nilai x = 0 untuk melihat hasilnya.
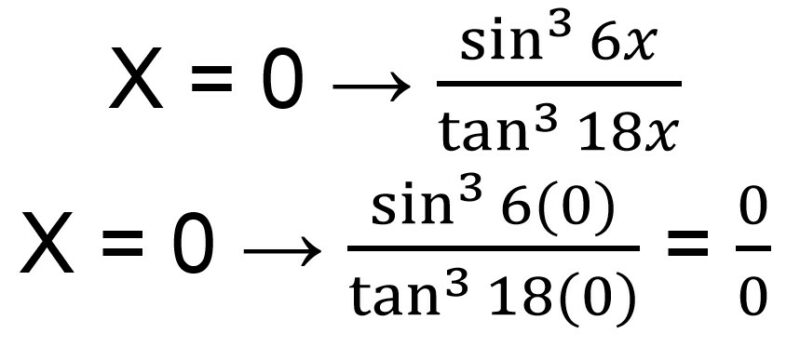
Dikarenakan hasil di atas adalah bentuk tak tentu, maka untuk mengerjakan soal di atas, kamu bisa menggunakan rumus limit trigonometri. Pada bentuk limit di atas, kamu bisa mengalikan pembilang dan penyebut dengan . Perkalian ini untuk mendapatkan bentuk
dan
.
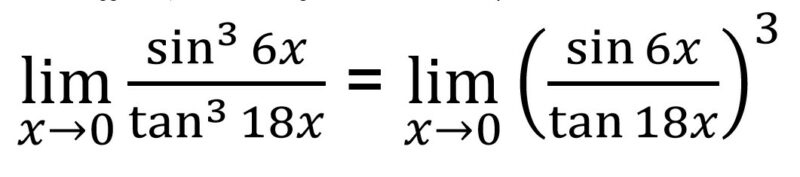
3. Tentukan hasil dari bentuk limit ![]()
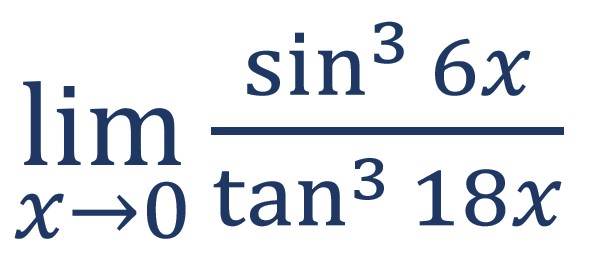
Untuk mengerjakan soal limit trigonometri, kamu bisa memasukkan nilai x = 0 untuk melihat hasilnya.
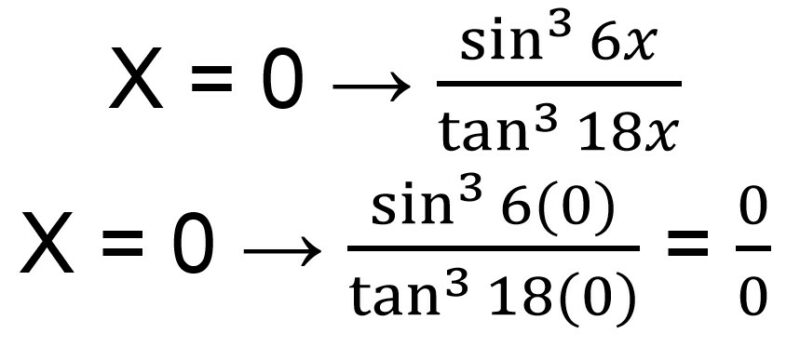
Jika kamu memasukkan nilai x = 0, maka bentuk akhirnya akan menjadi . Sehingga kamu harus menggunakan rumus limit trigonometri untuk mendapatkan hasil dalam bentuk tentu.
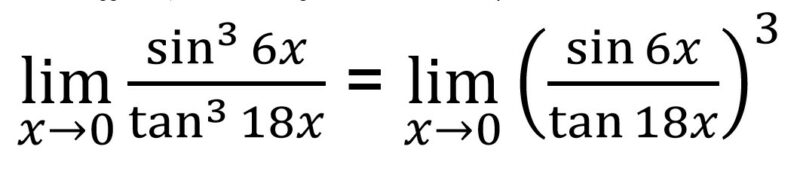
Kamu bisa menggunakan rumus di bawah ini dikarenakan memiliki kemiripan bentuk. Proses pengerjaannya seperti di bawah ini.
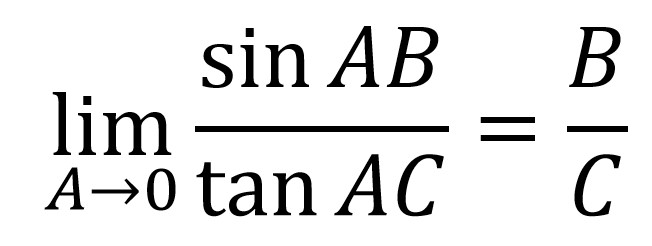
Sehingga di dapatkan nilai B = 6 dan nilai C = 18.
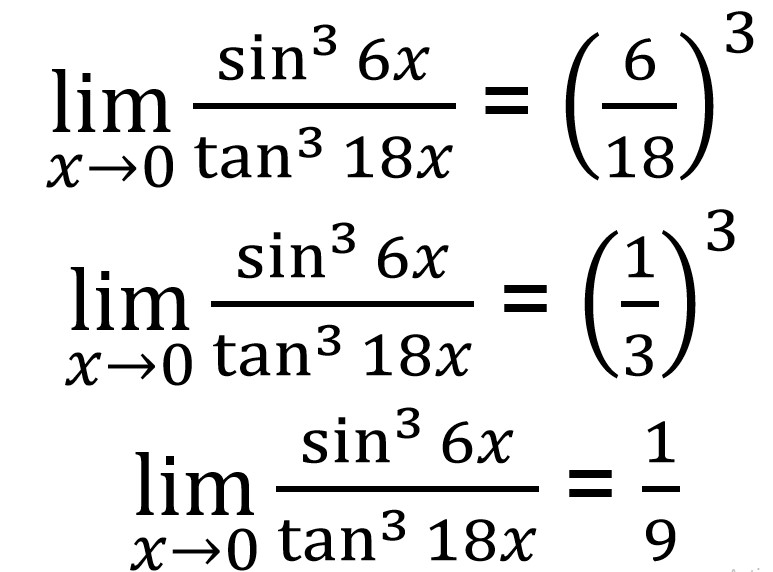
4. Tentukan hasil dari bentuk limit ![]()
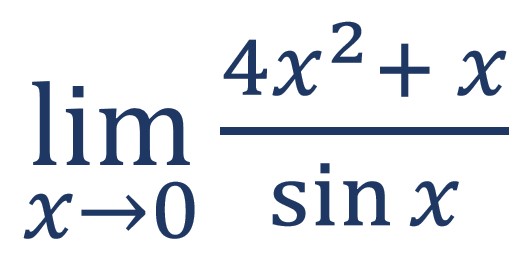
Langkah pertama yang bisa dilakukan adalah memasukkan nilai x = 0 untuk mengetahui bentuk dari limit tersebut.
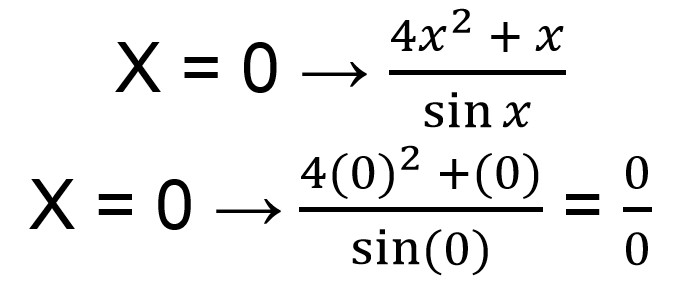
Ketika kamu memasukkan nilai x = 0, maka bentuk limit menjadi limit tidak tentu sehingga kamu harus memecah bentuk tersebut menjadi lebih sederhana.
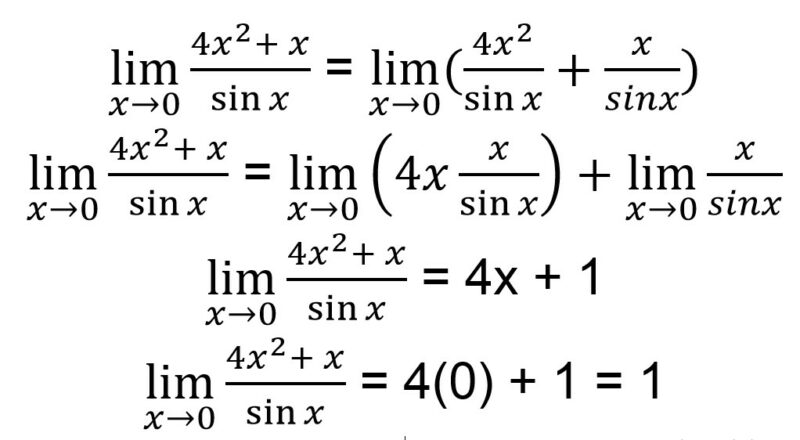
5. Berapakah hasil dari bentuk limit ![]()
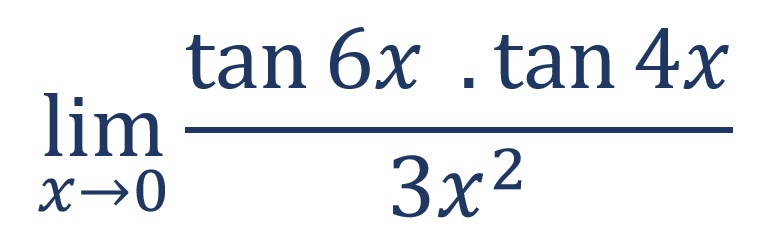
Langkah pertama yang bisa dilakukan adalah memasukkan nilai x = 0 untuk mengetahui bentuk dari limit tersebut.
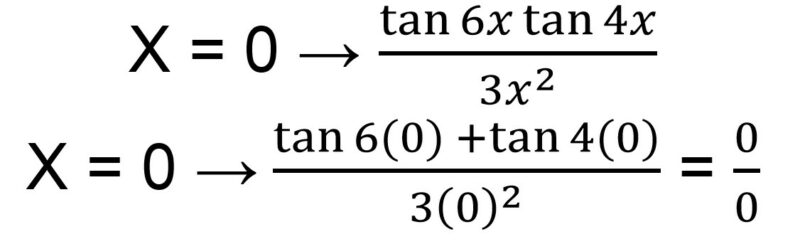
Dikarenakan bentuk akhir setelah dimasukkan nilai x = 0 menjadi tidak tentu, maka kamu bisa mengubah bentuk tersebut menjadi lebih sederhana seperti di bawah ini
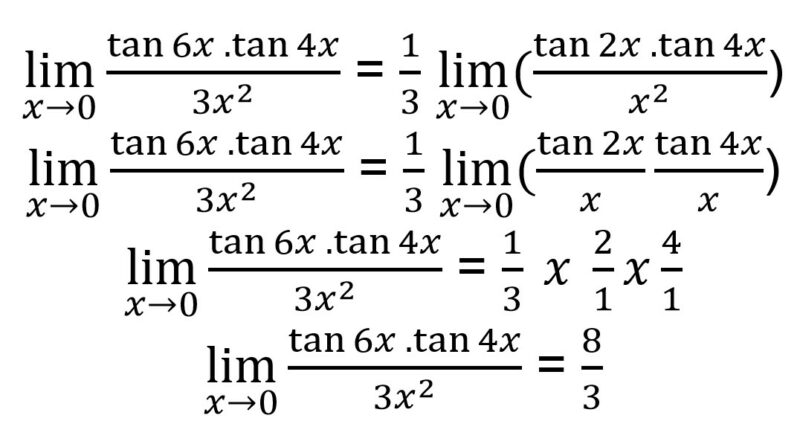
6. Tentukan hasil dari bentuk ![]()
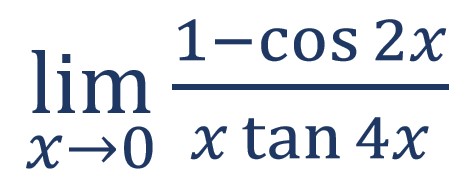
Untuk mengerjakan soal di atas, kamu perlu melakukan uji bentuk akhir dari limit tersebut dengan memasukkan nilai x = 0.
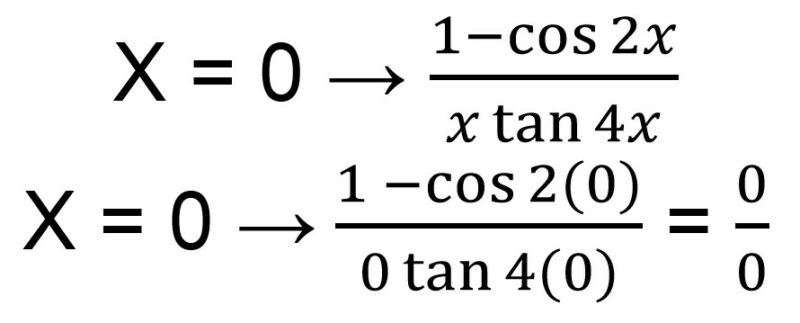
Bentuk akhir dari limit tersebut adalah bentuk tak tentu. Sehingga kamu harus mengubah bentuk tersebut menjadi lebih sederhana. Kamu bisa mengubah cos 2x terlebih dahulu.
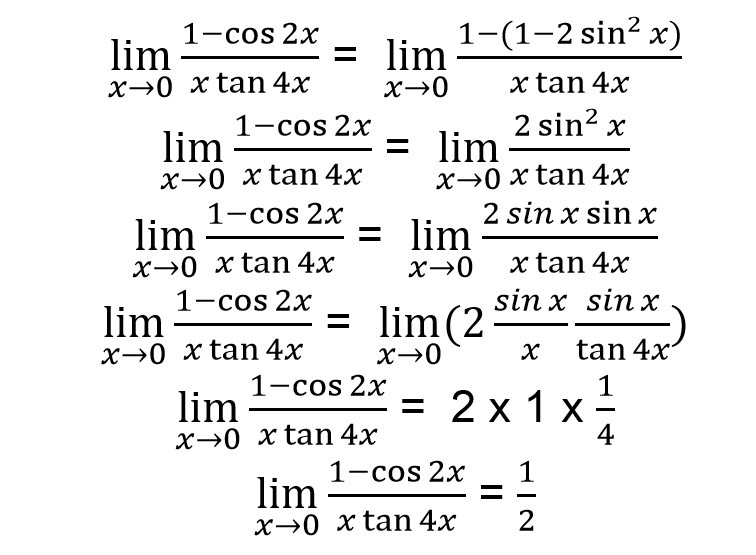
Cos 2x = 1 – 2 sin2 x
Sehingga kamu bisa memasukkan bentuk cos 2x ke dalam limit tersebut dan diperoleh seperti di bawah ini.
7. Berapakah hasil dari ![]()
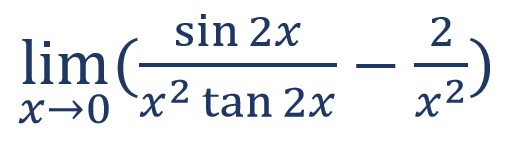
Langkah pertama yang perlu dilakukan adalah menguji bentuk dari limit tersebut dengan memasukkan x = 0.
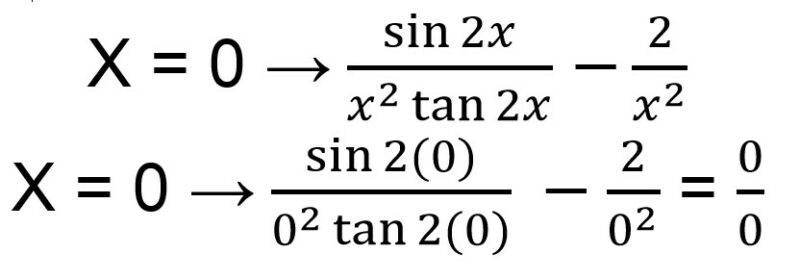
Jika nilai x = 0 dimasukkan ke dalam limit tersebut, hasilnya berubah menjadi bentuk tak tentu. Sehingga kamu bisa mengubah bentuk di atas menggunakan beberapa rumus trigonometri seperti di bawah ini.
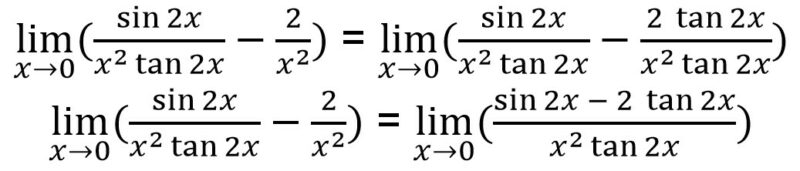
Karena bentuk limit di atas adalah tan 2x dan bentuk tan 2x = sehingga pecahan limit tersebut bisa dikalikan dengan
untuk mengubah bentuknya menjadi lebih sederhana.
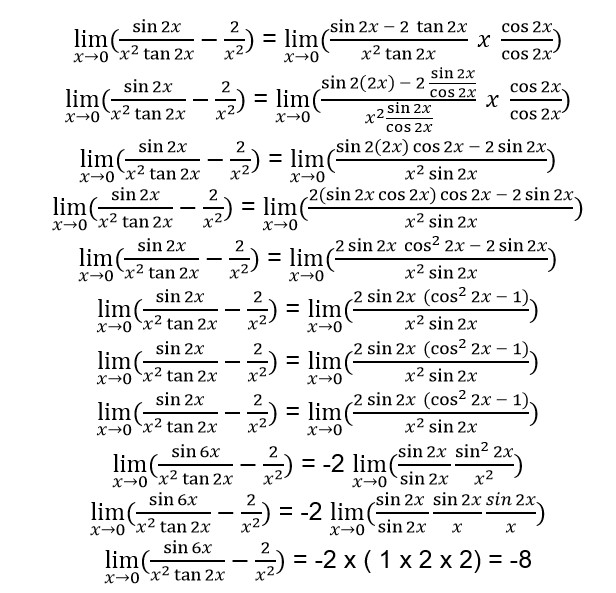
Belajar limit fungsi trigonometri membutuhkan langkah pembuktian bukti tak tentu dan mengubah bentuk limit trigonometri menjadi lebih sederhana. Semakin banyak belajar soal-soal, kamu akan terbiasa dengan rumus trigonometri untuk menyelesaikan persoalan limit trigonometri.
Baca Juga:
