Pada pembahasan kali ini, kamu akan belajar salah satu materi matematika yang memiliki banyak penerapan dalam kehidupan sehari-hari yaitu trigonometri. Trigonometri sendiri tersusun dari sifat trigonometri sin cos tan.
Kamu akan belajar tentang pengertian, rumus dan identitas geometri, tabel kuadran geometri, serta soal dan pembahasan yang berkaitan dengan geometri.
Pengertian Sin Cos Tan
Pembahasan pertama adalah pengertian dari fungsi trigonometri. Fungsi trigonometri sendiri menjelaskan tentang hubungan antara sudut-sudut yang membentuk sebuah segitiga.
Hubungan sudut-sudut yang membentuk segitiga kemudian dikenal sebagai sin cos tan. Hubungan antara 3 sudut ini bisa kamu lihat dalam gambar di bawah ini.
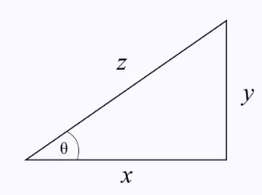
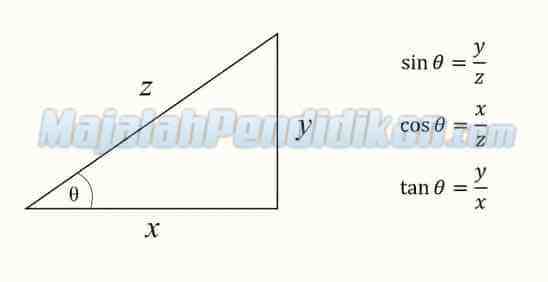
Simbol x, y, dan z menjelaskan tentang sinus, cosinus, dan tangen pada segitiga dengan θ sebagai sudut yang terbentuk.
- Sinus pada segitiga di atas adalah perbandingan antara tinggi segitiga y dengan sisi miring pada segitiga z.
- Cosinus pada segitiga di atas menjelaskan tentang perbandingan antara alas segitiga x dengan sisi miring pada segitiga z.
- Tangen pada segitiga di atas menjelaskan perbandingan antara tinggi segitiga y dengan alas segitiga x
Rumus di dalam Geometri
Setelah kamu belajar tentang pengertian dari hubungan sudut, maka kamu bisa melihat beberapa rumus yang digunakan di dalam trigonometri yang berhubungan dengan sinus, kosinus, dan tangen.
1. Rumus Dasar
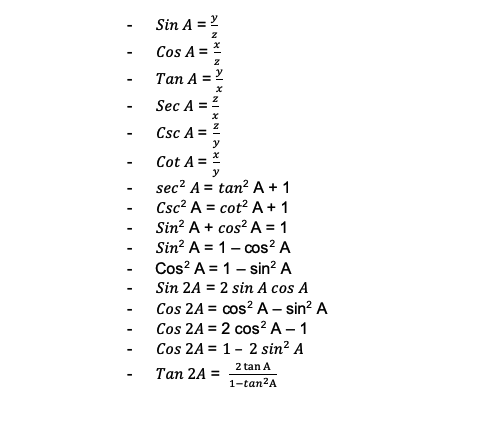
2. Rumus Penjumlahan Sudut
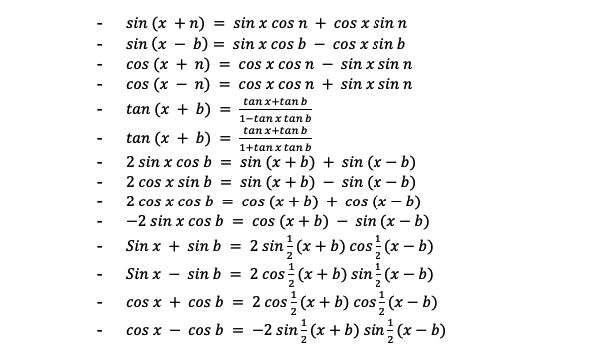
a. Aturan Sinus
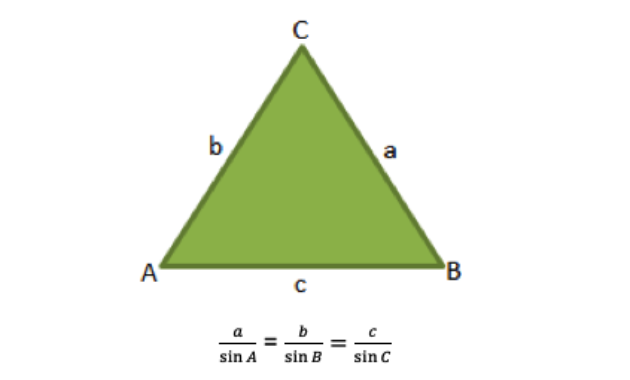
b. Aturan Cosinus
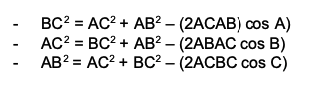
c. Aturan Tangen
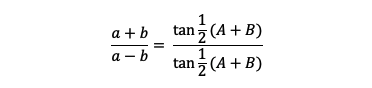
Tabel Kuadran Geometri
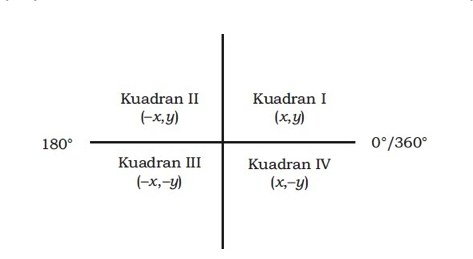
Setelah kamu mengetahui rumus yang digunakan dalam geometri, selanjutnya kamu akan belajar mengenai tabel kuadran pada geometri. Tabel kuadran ini digunakan untuk menentukan nilai positif atau negatif sudut yang terbentuk karena tidak semua nilai sinus, kosinus, dan tangen memiliki nilai yang positif.
1. Kuadran I
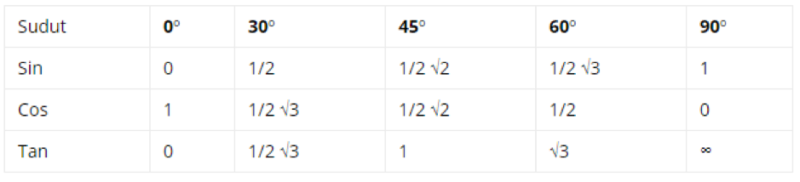
Kuadran I dalam tabel kuadran adalah bagian yang berada dalam rentang 0o ≤ θ ≤ 90o. Semua nilai perbandingan dalam sudut segitiga yang masuk ke dalam kuadran I akan bernilai positif.
2. Kuadran II

Kuadran II dalam tabel kuadran adalah bagian yang berada dalam rentang 90o ≤ θ ≤ 180o. Pada rentang ini, nilai x adalah negatif sehingga beberapa perbandingan akan memiliki nilai negatif pada kuadran II seperti di bawah ini.
3. Kuadran III
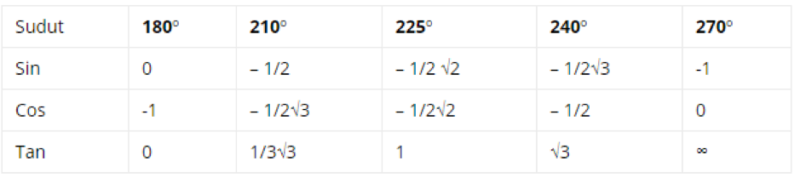
Kuadran III dalam tabel kuadran adalah bagian yang berada dalam rentang 180o ≤ θ ≤ 270o. Pada kuadran III, nilai pada sumbu x dan pada sumbu y memiliki nilai yang negatif sehingga beberapa hasil perbandingannya memiliki nilai negatif.
4. Kuadran IV
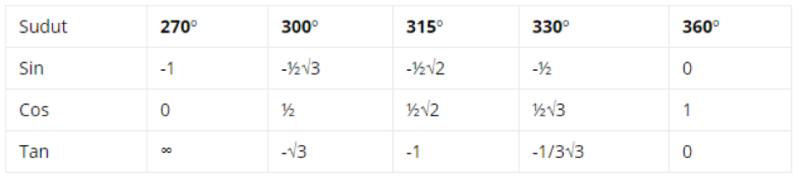
Kuadran IV dalam tabel kuadran adalah bagian yang berada dalam rentang 270o ≤ θ ≤ 360o. Pada kuadran IV, nilai pada sumbu x adalah positif dan pada sumbu y memiliki nilai yang negatif sehingga beberapa hasil perbandingannya memiliki nilai negatif.
Contoh Soal dan Pembahasan
Diberikan A = sin x + sin y dan B = cos x – cos y. Pada saat apakah nilai A2 + B2 memiliki nilai terbesar
Untuk mengerjakan soal ini kamu bisa menulis ulang informasi yang ada di dalam soal.
A = sin x + sin y → A2 = sin2 x + 2 sin x sin y + sin2 y
B = cos x – cos y → B2 = cos2 x – 2 cos x cos y + cos2 y
A2 + B2 = (sin2 x + 2 sin x sin y + sin2 y) + (cos2 x – 2 cos x cos y + cos2 y)
A2 + B2 = (sin2 x + cos2 x) + (2sin x sin y – 2 cos x cos y) + (sin2 y + cos2 y)
Dikarenakan sin2 x + cos2 x = 1, maka bentuk di atas menjadi seperti di bawah ini.
A2 + B2 = 1-2(sin x sin y – cos x cos y) + 1
A2 + B2 = 2-2 cos(x + y)
Dikarenakan bentuk A2 + B2 mengandung nilai cos, maka untuk mencari nilai A2 + B2 terbesar dapat menggunakan rentang paling kecil dan paling besar cos yaitu -1 dan 1. Sehingga kamu bisa masukkan nilai tersebut.
Cos (x+y) = 1 → A2 + B2 = 2 – 2 (1) = 0
Cos (x+y) = -1 → A2 + B2 = 2 – 2 (-1) = 4
Sehingga nilai terbesar A2 + B2 berada ketika nilai cos (x+y) sama dengan -1 atau x+y = 180o
Memahami materi sin cos tan memang tidak bisa dilakukan hanya sekali. Kamu perlu melakukan pengulangan dan berlatih pemahamanmu dengan mengerjakan soal dengan berbagai tingkat soal yang berbeda. Tujuannya adalah meningkatkan kemampuan dan pemahamanmu dalam memahami materi ini.
Baca Juga:
