Pada pembahasan kali ini, kamu akan mempelajari tentang materi macam macam pola bilangan dan contoh soalnya. Fenomena pola ini akan ditemui dalam kehidupan sehari-hari seperti bilangan prima, bilangan genap, bilangan, ganjil dan sebagainya.
Kamu akan mempelajari tentang materi ini lebih jauh mulai dari berbagai jenis pola yang ada beserta rumus yang digunakan untuk mencari nilai bilangan tertentu dalam suatu pola.
Pengertian Pola Bilangan Matematika
Sebelum lanjut lebih jauh, kamu akan belajar tentang pengertian dari pola suatu bilangan dalam matematika. Pola suatu bilangan menjelaskan tentang susunan angka yang dapat membentuk suatu pola sehingga kamu dapat mengetahui nilai bilangan pada suku ke-n dalam pola tersebut. Contoh sederhananya, kamu bisa mengetahui nilai suku ke-100 pada bilangan ganjil.
Macam Macam Pola Bilangan Matematika
Setelah kamu mengetahui pengertian pola suatu bilangan, saat ini kamu akan belajar tentang macam-macam pola yang terbentuk dari berbagai jenis bilangan seperti bilangan ganjil, genap, persegi, persegi panjang, segitiga, fibonacci, pangkat tiga, pascal, aritmatika, dan geometri.
Untuk pemahaman yang lebih jelas, kamu bisa menyimak materi tentang macam-macam pola suatu bilangan di bawah ini.
1. Bilangan Ganjil
Pola pertama yang akan kamu pelajari adalah pola dalam bilangan ganjil. Bilangan ganjil sendiri adalah bilangan asli yang tidak di habis dibagi oleh dua atau kelipatan dari dua seperti 1, 3, 5, 7 dan seterusnya. Pola yang terjadi pada bilangan ganjil biasanya digambarkan seperti di bawah ini.
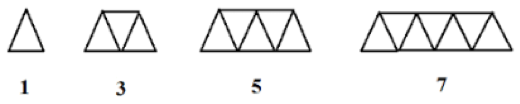
Dikarenakan terdapat pola di dalam bilangan ganjil, maka kamu bisa menggunakan rumus bilangan ganjil untuk mendapatkan nilai bilangan ganjil ke n seperti di bawah ini.
Un = 2n – 1
Semisal kamu ingin mencari nilai ke-13 dalam bilangan ganjil, maka kamu tinggal memasukkan nilai 13 ke dalam rumus tersebut seperti ini.
U(13) =(2.13) – 1 = 25
2. Bilangan Genap
Pola kedua yang akan kamu pelajari adalah pola dalam bilangan genap. Bilangan genap sendiri adalah bilangan asli yang habis jika dibagi dengan 2 atau kelipatan dari dua seperti 2, 4, 6, dan seterusnya. Biasanya pola dalam bilangan genap digambarkan seperti di bawah ini.
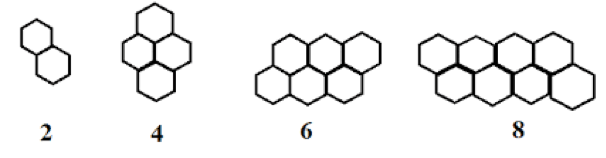
Dikarenakan terdapat pola dalam bilangan genap, maka kamu bisa menggunakan rumus di bawah ini untuk mencari nilai bilangan genap ke n.
Un = 2n
Jika kamu ingin mencari nilai ke-11 dari suatu bilangan genap, maka kamu bisa memasukkan angka 11 tersebut ke dalam rumus di atas.
U(11) = 2.11 = 22
3. Bilangan Persegi
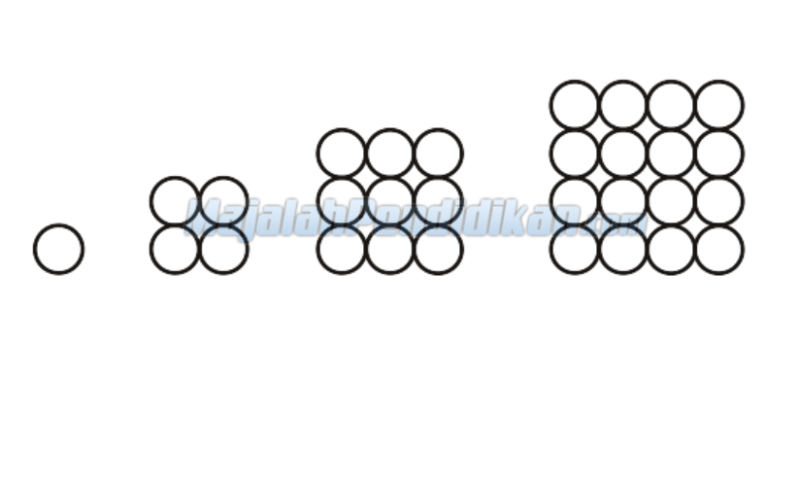
Pola ketiga yang akan kamu pelajari adalah pola dalam bilangan persegi. Bilangan persegi adalah kuadrat dari nilai suku yang akan kita cari seperti 1, 4, 9, 16, dan seterusnya. Biasanya bilangan persegi digambarkan seperti di bawah ini.
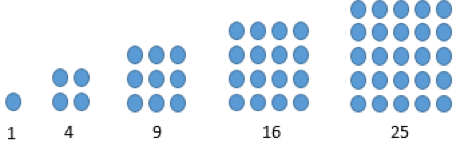
Dikarenakan dalam bilangan persegi terdapat pola, maka kamu bisa mencari nilai ke-n dalam bilangan persegi menggunakan rumus di bawah ini.
Un = n2
Misalkan kamu ingin mencari nilai suku ke-7 dalam bilangan persegi, maka kamu bisa memasukkan 7 ke dalam rumus tersebut.
U(7) = 72 = 49
4. Bilangan Persegi Panjang
Pola keempat yang akan kamu pelajari adalah pola suatu bilangan persegi panjang. Berbeda dengan bilangan persegi yang merupakan kuadrat dari nilai suku yang kamu cari, pada bilangan persegi kamu akan menemui bentuk bilangannya berbentuk persegi panjang seperti 2, 6, 12, 20, dan seterusnya.
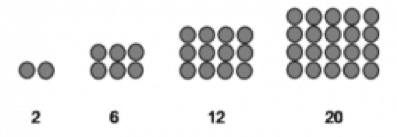
Dikarenakan dalam bilangan persegi panjang terdapat pola tertentu, maka untuk mencari nilai pada bilangan persegi panjang, kamu bisa menggunakan rumus di bawah ini.
Un = n(n+1)
Misalkan kamu ingin mencari nilai suku ke-9, maka kamu bisa memasukkan angka 9 ke dalam rumus di atas.
U(9) = 9(9+1) = 90
5. Bilangan Segitiga
Pola kelima yang akan kamu pelajari adalah pola suatu bilangan segitiga. Bilangan segitiga adalah bilangan yang membentuk segitiga seperti pada 1, 3, 6, 10, dan seterusnya. Pola suatu bilangan segitiga biasanya digambarkan seperti di bawah ini.

Dikarenakan dalam bilang segitiga terdapat suatu pola tertentu, sehingga kamu bisa menggunakan rumus di bawah ini untuk mencari nilai suku ke-n pada suatu bilangan segitiga.
Un = 1/2n x (n+1)
Misalkan kamu ingin mencari nilai pada suku ke-10, maka kamu bisa memasukkan nilai 10 ke dalam rumus tersebut.
U(10) = 1/2 x 10(10+1) = 55
6. Bilangan Fibonacci
Pola keenam yang akan kamu pelajari adalah pola dalam bilangan fibonacci. Bilangan fibonacci adalah bilangan yang setiap suku setelah angka satu merupakan penjumlahan dari dua suka di atasnya. Bilangan fibonacci seperti 1, 1, 2, 3, 5, 8, 13, 21, 34, dan seterusnya. Biasanya bilangan fibonacci digambarkan seperti di bawah ini.
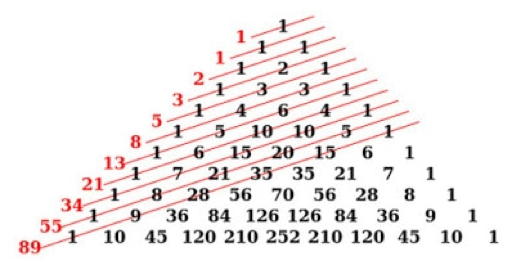
Untuk mendapatkan nilai tertentu pada pola dalam bilangan fibonacci, kamu bisa menggunakan rumus di bawah ini.
Un =Un-1 + Un-2
7. Bilangan Segitiga Pascal
Pola ketujuh yang akan kamu pelajari adalah pola dalam bilangan segitiga pascal. Seperti namanya, bilangan Pascal ditemukan oleh Blaise Pascal dengan susunan angkanya akan membentuk suatu segitiga. Bilangan segitiga pascal biasanya digambarkan seperti di bawah ini.
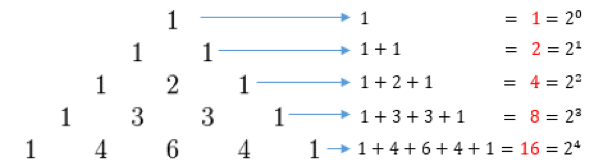
Dikarenakan dalam bilangan segitiga pascal terdapat pola tertentu, sehingga kamu mencari nilai suku ke-n pada bilangan segitiga pascal menggunakan rumus di bawah ini.
Un = 2n-1
Sehingga jika kamu ingin mencari nilai suku ke-8, maka kamu bisa memasukkan 8 ke dalam rumus tersebut seperti di bawah ini.
U(8) = 28-1 = 27 = 128
8. Bilangan Pangkat Tiga

Pola kedelapan yang akan kamu pelajari adalah pola dalam bilangan pangkat tiga. Bilangan pangkat tiga adalah bilangan yang terdiri dari hasil pangkat sebelumnya seperti pada 1, 8, 27, 64, dan seterusnya. Untuk rumus yang digunakan dalam pola suatu bilangan pangkat tiga bergantung terhadap pola sederhana dari bilang tersebut.
Un = n3 → 1, 8, 27, 64, …..
Un = (Un-1)3 → 2, 8, 512, ….
9. Bilangan Aritmatika

Pola bilangan yang kesembilan yang akan kamu pelajari adalah bilangan aritmatika. Bilangan aritmatika adalah bilangan yang memiliki selisih yang sama di tiap sukunya seperti pada 1, 4, 7, 11, dan seterusnya. Untuk mencari nilai dalam suku ke-n suatu bilangan aritmatika, maka kamu bisa menggunakan rumus di bawah ini.
Un = a + (n-1)b
Keterangan:
- a adalah suku awal/nilai awal biasanya disebut sebagai U1
- b adalah beda tiap suku
10. Bilangan Geometri

Pola bilangan terakhir yang kamu pelajari adalah bilangan geometri. Bilangan geometri adalah bilangan yang terdiri dari perkalian antara suku sebelumnya dengan rasio yang tetap. Bilangan geometri seperti 1, 2, 4, 8, 16, dan seterusnya. Untuk mencari suku ke-n dalam bilangan geometri bisa menggunakan rumus di bawah ini.
Un = arn-1
Misal sebuah bilangan geometri adalah 1, 2, 4, 8, 16, dan seterusnya, maka jika kamu ingin mencari nilai suku ke-9, tinggal memasukkan angka 9 ke dalam rumus.
U(9) = 1.29-1 = 256
Belajar macam macam pola bilangan dapat membantumu untuk memahami susunan bilangan yang cukup panjang, sehingga kamu bisa lebih cepat untuk mencari nilai suku tertentu dalam suatu susunan bilangan.
Baca Juga: