Rumus Volume Tabung – Pada kesempatan ini majalahpendidikan.com akan membahas perihal bangun ruang pada tabung. untuk bangun ruang pada tabung sendiri mempunyai banyak jenis diantaranya yaitu masih banyak jenisnya, tabung tanpa tutup, dan tabung tidur.
Tabung atau juga memiliki istilah lain yakni silinder memiliki beberapa rumus diantaranya adalah luas permukaan, rumus luas alas, luas permukaan tanpa tutup, luas selimut dan volume.
Nah untuk kali ini kami akan menjabarkan materi yakni tentang bagaimana cara untuk menghitung volume tabung dengan mudah melalui diameter atau juga dengan tidak mengetahui angka diameternya.
Sebelum beranjak ke materinya pertama – pertam yang akan kita bahas terlebih dahulu yakni pengertian tabung, dan berikut ini pembahasan singkat tentang tabung.
Pengertian

Perlu kalian ketahui Tabung adalah bangun ruang yang memiliki batas antara dua sisi yang biasa disebut kongruen dan juga sejajar yang memiliki bentuk lingkaran serta ada sebuah sisi lengkung.
Banyak juga yang belum mengerti dan memahami dengan baik tentang suatu penyelesaian perihal volume tabung, baik itu dari Definisi, atau unsur-unsur maupun Penentuan Rumus-rumus yang ada Pada tabung.
Sifat – Sifat Tabung
- Tabung tidak mempunyai titik sudut
- Mempunyai 2 rusuk lengkung
- Mempunyai 3 bidang sisi
- Bidang selimut
- Bidang tertutup
- Bidang alas
Unsur -Unsur Tabung
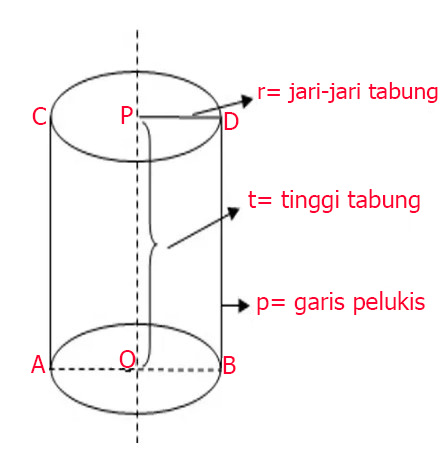
Selanjutnya yaitu kami akan menjabarkan perihal tentang unsur – unsur dari tabung, simak baik – baik penjelasannya berikut ini :
1. Jari – Jari Tabung
Jari jari merupakan jarak setengah pada tabung contohnya dapat kalian lihat diatas dari titik P menuju titik D, jarak setengah itulah yang dinakaman jari-jari, jari – jari pada tabung memiliki istilah dalam rumus matematika yakni r= Jari-Jari Tabung.
2. Tinggi Tabung
Tinggi tabung dapat kalian lihat yakni dari titik O menuju titik P, dalam soal jika ada nilai dari O menuju P berarti itu merupakan tinggi dari tabung tersebut, tinggi pada tabung memiliki istilah dalam rumus matematika yakni t= Tinggi Tabgung.
3. Garis Pelukis
Sama seperti namanya yakni Garis Pelukis merupakan garis yang menggambarkan bentuk dari tabung maka dengan kata lain garis yang menggambarkan tabung dapat disebut dengan garis pelukis.
4. Diameter
Diameter pada tabung dapat dilihat pada titik A menuju titik B, itulah yang dapat dikatakan sebagai diameter tabung.
5. Sisi
Yang dapat dikatakan sebagai sisi yakni lingkaran dengan pusat yang berada dari titik yang ada di tengah menuju sisi yang ada diatas yakni sisi yang memiliki bentuk lingkaran pada tabung yang memiliki titik pusat berada ditengah pada tabung.
Rumus Volume Tabung
Dibawah ini merpakan rumus penjabaran yang ada pada volume tabung, simak baik-baik dan apabila perlu bisa kalian catat untuk menambah pembelajaran tentang pelajaran matematika.
| Jenis | Rumus |
| Luas Alas | LA= π × r × r |
| Luas Permukaan | L=2 × π × r × (r + t) |
| Luas Selimut | LS=π × d × t |
| Volume | V=π × r² × t |
| Luas Tanpa Tutup | Ltanpa tutup= LA + LS |
| Volume Kerucut+Tabung | ( π x r2 x t)+( 1/3 x π x r2 x t ) |
| Luas Kerucut+Tabung | (π x r2 )+(2 x π x r x t)+( π x r x s ) |
Keterangan dari rumus diatas
- V =volume tabung yaitu (cm3)
- π =phi yaitu (22/7 atau 3,14)
- r =jari – jari/setengah diameter yaitu (cm)
- t =tinggi yaitu (cm)
Contoh Soal Volume Tabung
Contoh soal 1 :
1. Sebuah tabung mempunyai sebuah jari – jari dan juga tinggi yang memiliki masing – masing 20 cm dan 40 cm, maka tentukan lah berapa angka volume yang ada pada tabung tersebut?
Di ketahui :
r =20 cm
t =40 cm di tanya :
volume dari tabung tersebut yaitu ? volume = π x r2 x t
Jawabannya :
=3,14 x 20 cm x 20 cm x 40 cm
= 5.024 cm3 Jadi, volume pada tabung diatas adalah 5.024 cm3
Contoh Soal 2 :
2. Sebuah tabung mempunyai jari – jari 20 cm dan tinggi nya 40 cm, maka tentukan lah berapa angka luas yang ada pada tabung tersebut?
Di Ketahui :
r = 20 cm
t = 10 cm
Luas dari tabung tersebut yaitu ? Luas =2 x π x r (r+t)
Jawabannya :
=2 x 22/7 x 20 cm x 10 cm (20 cm + 10 cm)
=2 x 44 cm x 10 cm (30 cm)
=26400 cm2
Jadi, luas nya adalah 26400 cm2
Demikian lah pembasan mengenai rumus volume pada tabung mulai dari, pengertian, sifat – sifat, unsur – unsur, rumus, contoh soal, semoga dengan adanya artikel ini dapat bermanfaat untuk kita semua dan menambah pengetahuan tentang pelajaran matematika, Terima Kasih.
Baca Juga :