Halo sobat semua artikel ini membahas tentang Bilangan Eksponen mulai dari pengertian, bentuk, fungsi, sifat, dan contoh soalnya.
Eksponen ini seringkali dipakai oleh para peneliti agar memudahkan dalam menulis suatu angka. Contohnya saja, ada seseorang peneliti luar angkasa yang melakukan pengukuran jarak bumi dan mars.
Kalian tahu kan seberapa jauh jaraknya? Ya, jaraknya itu berjuta-juta kilometer. Nah agar mudah dalam menulisnya, maka si peneliti memakai eksponen.
Jadi, jarak yang dimana berjuta-juta tadi itu, oleh peneliti ditulis didalam bentuk eksponen. Nah seperti apa sih bilangan eksponen itu? Yuk, simak pembahasannya di bawah ini.
Pengertian Dari Bilangan Eksponen

Bilangan Eksponen yakni bentuk suatu bilangan perkalian dan bilangan yang sama lalu di ulang-ulang atau pengertian singkatnya ialah perkalian yang diulang-ulang.
Bilangan ini biasanya dipakai secara luas di berbagai bidang misalnya saja dalam bidang kimia, ekonomi, biologi, fisika, dan juga ilmu komputer.
Dengan aplikasi misalnya perbungaan, pertumbuhan dari jumlah penduduk, perilaku – perilaku gelombang, kinetika kimia, dan juga kriptografi kunci publik (ilmu yang dimana mempelajari soal cara supaya pesan ataupun dokumen seseorang itu aman serta tak terbaca oleh orang lain yang tak berhak untuk membacanya).
Contoh:
an = a x a x a x…x a (a dikalikan sama dengan jumlah n)
Contohnya saja :
25 = 2 x 2 x 2 x 2 x 2 yang hasilnya adalah 32
Bentuk Bilangan Eksponen
Didalam bilangan eksponen atau bisa dibilangan juga bilangan pangkat itu tak selamanya selalu mempunyai nilai bulat positif tetapi dapat juga bernilai nol, negatif atau pecahan.
- Bilangan Eksponen Pecahan
Rumus = a1/n = n√a
Contoh:
21/2 = √2
21/3 = 3√2
- Bilangan Eksponen Nol
Apabila a ≠ 0 jadi a = 1 atau a tak boleh sama dengan 0.
contoh:
3 =1
7 =1
128 =1
y =1
- Bilangan Eksponen Negatif
Apabila m dan juga n ialah bilangan bulat positif jadi rumusnya a-n = 1/an
contoh:
3-4 = 1/34 = 1/81
Bentuk Persamaan Eksponen
Bentuk persamaan eksponen yakni persamaan yang didalamnya ada pangkat-pangkat yang dimana berbentuk sebagai fungsi didalam x yang dimana x ialah sebagai bilangan pengubah.
Rumus:
- af(x) = 1 ( Apabila af(x) = 1 dan a>0 serta a ≠0, jadi f (x) = 0)
- af(x) = ag(x) (Apabila af(x) = ag(x) dan a>0 serta a ≠0, jadi f (x) = g(x))
- af(x)= ap (Apabila af(x) = ap dan a>0 serta a≠0, jadi f(x) = p)
- af(x)= bf(x) (Apabila af(x) = bf(x) dan a>0 dan a ≠1, b>0 dan b ≠1, dan a≠b jadi f(x) = 0)
- A (af(x))2 + B(af(x)) + C = 0 (Dengan af(x) = p, maka bentuk dari persamaan itu bisa dirubah kedalam persamaan kuadrat yakni Ap2 + Bp + C = 0)
Fungsi Eksponen dan juga Grafiknya
Fungsi eksponen yakni pemetaan bilangan real x ke dalam bilangan ax dengan a > 0 dan juga a ≠ 1. Apabila a > dan a ≠ 1, x∈R jadi f:(x) = ax lalu disebut dengan fungsi eksponen.
Fungsi eksponen dari, y = f(x) = ax : a > 0 dan juga a ≠ 1 memiliki beberapa sifat-sifat yakni sebagai berikut:
- Kurva yang terletak di atas sumbu x atau definit positif
- Memotong sumbu y pada titik ( 0,1 )
- Memiliki asimtot datar y = 0 (sumbu x). Arti dari asimtot ialah garis yang itu sejajar dengan sumbu x.
- Grafik monoton naik bagi bilangan x > 1
- Grafik monoton turun bagi bilangan 0 < x < 1
Gambar diatas ialah contoh bentuk grafiknya.
Contoh Soalnya:
Apabila f(x) = 2x+1 maka tentukanlah nilai dari f(3) dan juga f(-3)
f(3) = 23+1 = 24 = 16
f(-3) = 2-3+1 = 2-2 = 1/4 = 0,25
Sifat-Sifat Dari Bilangan Eksponen
Ada beberapa sifat yang dapat kita ketahui didalam memahami bilangan eksponen yakni di antaranya:
- Pertama
am . an = nm + n (apabila soalnya dikali untuk pangkatnya harus ditambah)
Contoh: 52 . 53 = 52 + 3 = 55
- Kedua
am : an = am – n (tapi apabila dibagi maka sebaliknya pangkatnya dikurang)
Contoh: 55 : 53 = 55 – 3 = 52
- Ketiga
( am )n = am x n (apabila soalnya di dalam kurung maka pangkatnya itu dikalikan)
Contoh: (52)3 = 52 x 3 = 56
- Keempat:
(a . b)m = am . bm
Contoh: (3 . 6)2 = 32 . 62
- Kelima
Untuk Sifat yang ke lima ini, syaratnya yaitu “b” ataupun penyebutnya tak boleh nol (0).
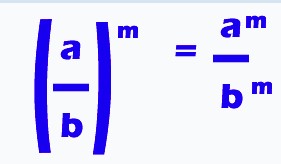
Contoh:
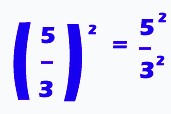
- Keenam
Di sifat yang ke enam ini, apabila (an) dibawahnya itu bilangan positif, maka disaat dipindahkan ke atas akan berubah menjadi negatif.
Begitupun sebaliknya, apabila (an) dibawah itu ialah negatif, jadi saat dipindahkan ke atas maka otomatis akan berubah menjadi positif. Mari kita lihat rumus serta contohnya dibawah ini:

- Ke tujuh
Disifat yang ketujuh ini, kita dapat melihat bahwa ada akar n dari am. Apabila pada saat disederhanakan, maka akar n bisa menjadi penyebut dan juga akar m bisa menjadi pembilang. Dengan syarat n harus jauh lebih besar sama dengan 2. Contoh rumusnya yaitu:
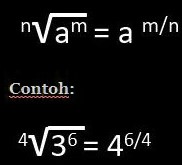
- Ke delapan
Bilangan eksponen nol mislanya a = 1.
Contoh:
2 = 1
6 = 1
9 = 1
Syaratnya a tak boleh nol.
Demikianlah yang dapat admin sampaikan materi ini dimana pembahasan mengenai Bilangan Eksponen. Semoga dengan materi yang sudah dibahas melalui artikel ini, dapat memberikan pemahamaan dan manfaat untuk sahabat pembaca semua.
Baca Juga:
