Halo sobat semua artikel ini membahas tentang definisi, sifat perkalian, sifat persamaan dan contoh dari Persamaan Nilai Mutlak.
Nilai mutlak didalam kalkulus sangatlah berguna agar dapat menyelesaikan berbagai macam persoalan matematika, baik itu dalam persamaan ataupun pertidaksamaan. Berikut ini ialah penjelasan lengkap soal nilai mutlak beserta contoh dan pembahasannya.
Definisi Nilai Mutlak
Persamaan nilai mutlak yakni nilai mutlak dari sebuah angka yang bisa didefinisikan sebagai sebuah jarak angka yang berada di atas titik 0 digaris angka tanpa perlu untuk memperhatikan bagaimanakah arahnya.
Nilai mutlak dari suatu angka x juga bisa diartikan sebagai suatu jarak angka di atas titik 0 digaris angka yang terlepas dari bagaimanakah itu terjadi. Ini artinya bahwa sanya | x | = 5 mempunyai dua solusi.
Itu dikarenakan terdapat dua angka yang dimana jaraknya di atas 0 ialah 3: x = -3 serta x = 5. Perhatikanlah gambar garis yang ada dibawah ini:
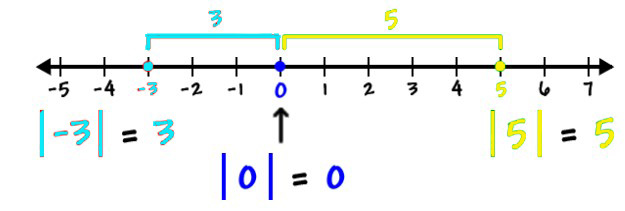
Konsep ini bisa diperluas sebagai situasi yang dimana melibatkan bentuk-bentuk aljabar yang ada di dalam sebuah simbol dari nilai mutlak.
Sifat Perkalian Dari Persamaan Nilai Mutlak

Jika A dan juga B ialah suatu bentuk aljabar, maka bentuknya seperti ini |AB| = |A||B|.
Perhatikan apabila A = –1 maka berdasarkan sifat itu|–B| = |–1||B| = |B|. Yang secara umum, sifat itu berlaku bagi sembarang konstanta A.
- Contoh soal memakai sifat perkalian dari persamaan nilai mutlak
Tentukanlah selesaian dari persamaan berikut ini: |–2x| + 5 = 15.
Pembahasannya kita harus terlebih dulu mengisolasi simbol dari nilai mutlak baru bisa mengaplikasikan sifat-sifat dari persamaan nilai mutlak tersebut.
|-2x| + 5 = 15
⇒ |-2x| = 10
⇒ |-2||x| = 10
⇒ 2|x| = 10
⇒ |x| = 5
x = -5 atau x = 5
Sifat Persamaan Dari Nilai Mutlak
Jika X ialah sebuah bentuk aljabar kemudian k ialah bilangan real positif, jadi |X| = k bisa mengimplikasikan X = –k ataupun X = k.
Seperti yang sudah dinyatakan didalam sifat persamaan ini, sifat ini hanya bisa diterapkan sesudah kita mengisolasi sebuah simbol disatu ruas. Untuk lebih jelasnya mari perhatikan contoh dibawah ini.
- Contoh 1
Selesaikanlah persamaan berikut ini : –2|x – 7| + 3 = 15.
Pembahasan Pertamanya, kita harus isolasi dulu nilai mutlak, yakni membuat simbol dari nilai mutlak yang berada disatu ruas lalu suku-suku lainnya kita bisa letakkan di ruas yang di bagian lainnya.
-2|x – 7| + 3 = 15
⇒ -2|x – 7| = 12
⇒ |x – 7| = 3
Sekarang kalian perhatikan bahwa sanya x – 7 ialah “X” disifat persamaan dari nilai mutlak, sehingganya
x – 7 = -3 atau x – 7 = 3
x = 4 atau x – 7 = 10
Dengan cara mensubstitusi ke dalam persamaan semula bisa dipastikan bahwa sanya himpunan penyelesaiannya ialah {3, 10}.
Catatan pada persamaan diatas 1 di atas, hati-hati agar tak memperlakukan simbol dari nilai ini misalnya tanda kurung biasa.
Persamaan dari –2(x – 7) + 3 = 15 hanya mempunyai selesaian x = 10, serta tak mempunyai penyelesaian kedua dikarenakan persamaan itu mempunyai bentuk yang sederhana x – 7 = 3.
Pada persamaan –2(x – 7) + 3 = 15 bisa disederhanakan menjadi |x – 7| = 3 yang mempunyai dua penyelesaian.
Persamaan ini bisa muncul dari berbagai macam bentuk. Tetapi dalam menyelesaikan persamaan itu, kita harus terus mengisolasi simbol dari nilai mutlak barulah setelah itu menerapkan sifat dari persamaan nilai mutlak tersebut.
- Contoh 2
Tentukanlah himpunan selesaian dari persamaan dibawah ini:
|5 – 2/3 x| – 9 = 8.
Pembahasannya yakni menggunakan cara mengisolasi simbol dari nilai mutlak barulah menerapkan sifat dari persamaan ini kita bisa mendapatkan
|5 – 2/3x| – 9 = 8
⇒ |5 – 2/3x| = 17
⇒ 5 – 2/3x = -17 atau 5 – 2/3x = 17
⇒ – 2/3x = -22 atau – 2/3x = 12
⇒ x = 33 atau x = -18
Sehingganya, himpunan penyelesaian dari persamaan itu ialah {–18, 33}.
Dan itulah pembahasan definisi dan sifat-sifatnya, untuk pembahasan selanjutnya yaitu beberapa contoh soalnya agar materi ini bisa kalian kuasai dengan baik.
Contoh Soal Persamaan Nilai Mutlak
1. Dalam bentuk ini tedapat dua penyelesaian.
(*) 2x + 2 = 6 , jadi 2x = 6 – 2
2x = 4 <==> x = 2
(**) 2x + 2 = -6 , maka 2x = -6 -2
2x = -8 <==> x = -4
Jadi, himpunan penyelesaiannya ialah {-4,2}
2. Perhatikanlah bentuk aljabar yang ada di dalam tanda mutlak, yakni 3x + 4. Penyelesaian dari persamaan nilai mutlak ini dapat dibagi menjadi 2 bagian.
Bagian yang pertama pada batasan 3x + 4> = 0 ataupun x >= -4/3
Bagian yang kedua pada batasan 3x + 4< 0 ataupun x < -4/3
Marilah kita selesaikan.
(*) pada x >= -4/3
Persamaan dari mutlak bisa ditulis:
(3x+4) = x–8
3x–x = -8–4
2x =-12
x = -6 (tak terpenuhi, dikarenakan batasan >= -4/3)
(**) pada x < -4/3
Persamaan mutlak bisa ditulis:
-(3x+4) = x–8
-3x–4 = x-8
-3x–x = -8+4
-4x = -4
x = 1 (tak terpenuhi, dikarenakan batasan < -4/3)
Jadi, tak terdapat himpunan penyelesaiannya.
3. Cara menyelesaikan soal pertidaksamaan mutlak ini bisa dibagi menjadi 2 bagian.
(*) 2x–3 >= 7
2x >= 7+3
2x >= 10
x >= 5
(**) 2x–3 <= -7
2x <= -7+3
2x <= -4
x <= -2
Jadinya, himpunan penyelesaiannya yakni { x/ x <= -2 ataupun x >= 5}
Demikianlah yang dapat admin sampaikan materi ini dimana pembahasan mengenai Persamaan Nilai Mutlak. Semoga dengan adanya materi yang sudah dibahas dalam artikel ini, bisa memberikan suatu pemahamaan dan juga manfaat untuk sahabat pembaca semua.
Baca Juga:
