Pada pembahasan kali ini, kamu akan belajar mengenai jenis-jenis dan operasi hitung dari suatu bilangan berpangkat. Materi ini memudahkan kamu untuk menulis bentuk perkalian atau pembagian yang memiliki banyak faktor perkalian atau pembagian. Berikut materi selengkapnya yang bisa kamu baca di bawah ini.
Pengertian Bilangan Berpangkat
Pembahasan pertama pada materi ini adalah pengertiannya. Suatu bilangan yang mempunyai banyak faktor perkalian yang sama akan menyusahkan dalam penulisannya. Misalkan kamu ingin menulis perkalian 5 x 5 sebanyak 20 kali. Tentu saja kamu akan kewalahan jika menuliskan semua perkalian tersebut hingga 20 kali.
Untuk memudahkan dalam penulisan perkalian berulang tersebut, kamu bisa menggunakan bilangan yang berpangkat. Sehingga kamu tidak perlu untuk menulis sebanyak 20 kali. Kamu bisa menulisnya lebih sederhana menjadi 520. Penulisan perkalian berulang menjadi bentuk tersebut akan menghemat waktu pengerjaan dan penulisan operasi hitungnya.
Bentuk umum dari perkalian berulang yang disederhanakan menjadi bilangan yang memiliki pangkat sesuai banyak faktor perkalian seperti di bawah ini.
5 x 5 x 5 x 5 x 5 x 5 = 56
Ay = A x A x A x A x A ……. sebanyak y kali
Keterangan :
- y adalah pangkat dari bilangan eksponen/berpangkat
- A adalah basis bilangan
Bentuk umum tersebut kemudian dibagi menjadi beberapa jenis sesuai dengan pangkatnya, baik bilangan bulat positif, bilangan bulat negatif, atau nol. Nama lain dari perkalian berulang ini adalah bilangan eksponen.
Jenis-Jenis

Setelah kamu belajar tentang pengertian dari bilangan yang berpangkat atau bilangan eksponen, selanjutnya kamu akan belajar tentang berbagai jenis bilangan eksponen. Pangkat pada bilangan eksponen dibedakan berdasarkan jenis bilangannya yaitu bilangan bulat positif, bilangan bulat negatif, nol, dan berpangkat pecahan.
1. Bilangan yang Berpangkat Bulat Positif
Jenis pertama yang akan dibahas adalah pangkat bulat positif. Sesuai dengan namanya, bilangan ini memiliki pangkat berupa bilangan bulat positif. Bilangan yang memiliki pangkat bulat positif biasanya terdiri dari bilangan real dan bilangan bulat positif sebagai pangkatnya. Berikut beberapa sifat dari bilangan yang pangkat bulat positif.
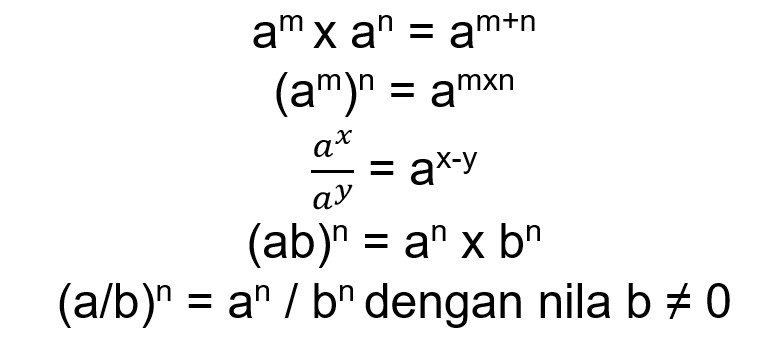
Kamu bisa melihat contoh di bawah ini untuk memahami sifat dari pangkat bulat positif di atas.
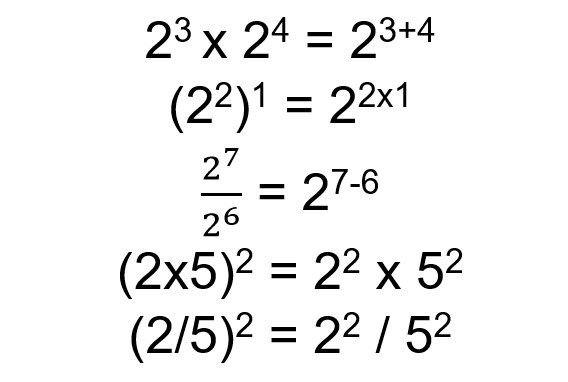
2. Bilangan yang Berpangkat Bulat Negatif
Pembahasan selanjutnya adalah bilangan yang memiliki pangkat bulat negatif. Seperti namanya, bilangan ini memiliki pangkat bulat negatif, sehingga untuk penulisannya menjadi keterbalikan dari pangkat negatifnya. Untuk lebih jelasnya, kamu bisa melihat sifat pangkat bilangan bulat negatif di bawah ini.
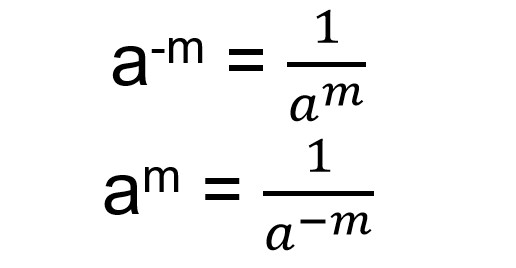
Untuk memahami kondisi di atas, kamu bisa melihat contoh di bawah ini.
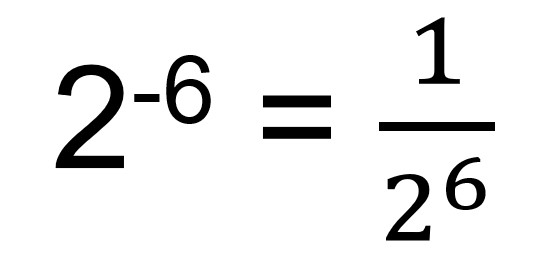
3. Bilangan yang Berpangkat Nol
Pembahasan ketiga adalah bilangan yang berpangkat nol. Bilangan yang memiliki pangkat nol akan menghasilkan angka 1 sebagai hasil akhirnya. Untuk bentuk dari bilangan yang berpangkat nol seperti di bawah ini.
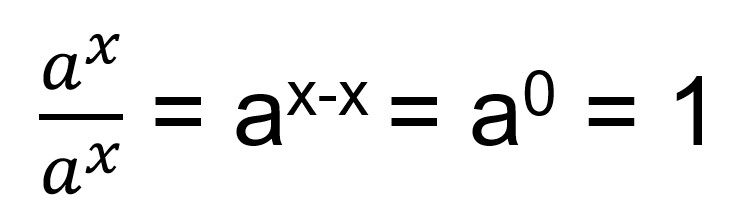
Bentuk di atas memiliki syarat untuk nilai a ≠ 0, karena jika nilai a = 0 maka hasil pangkatnya adalah seperti di bawah ini.

4. Bilangan yang Berpangkat Pecahan
Pembahasan keempat adalah bilangan yang berpangkat pecahan. Bilangan yang memiliki pangkat pecahan akan memiliki bentuk akar. Untuk memahaminya dengan jelas, kamu bisa melihat bentuk umum dari bilangan yang berpangkat pecahan.
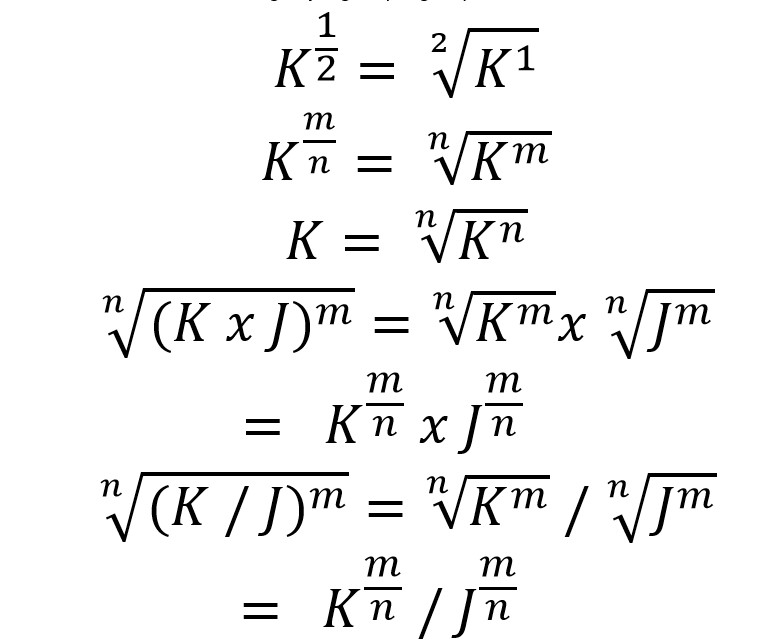
Kamu bisa melihat contoh di bawah ini untuk memahami bentuk di atas.
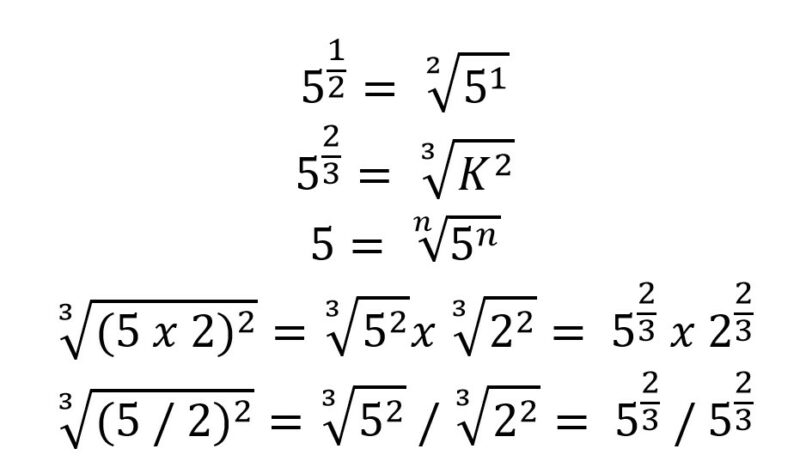
Contoh Soal Bilangan yang Berpangkat
1. Tentukan hasil perhitungan dari
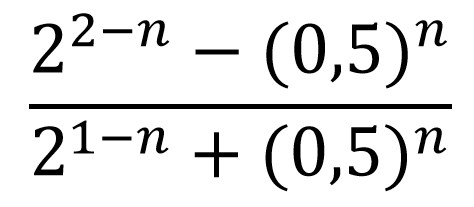
Untuk mengerjakan soal di atas, kamu harus mengingat aturan sifat bilangan yang berbilang seperti di bawah ini.
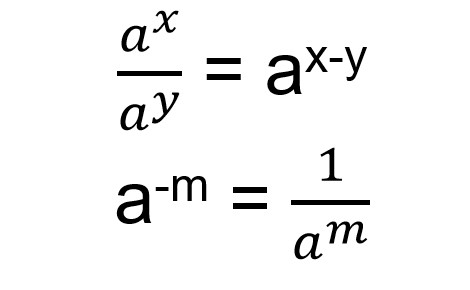
Sehingga untuk mengerjakan soal di atas, kamu bisa mengubah bentuk tersebut menjadi bentuk pembagian.
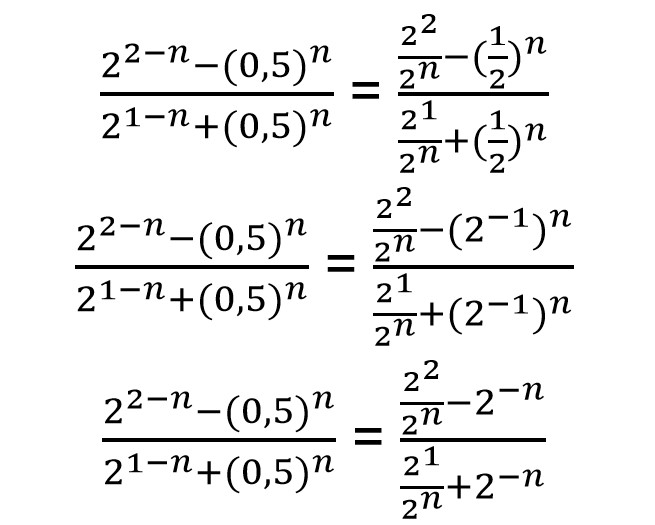
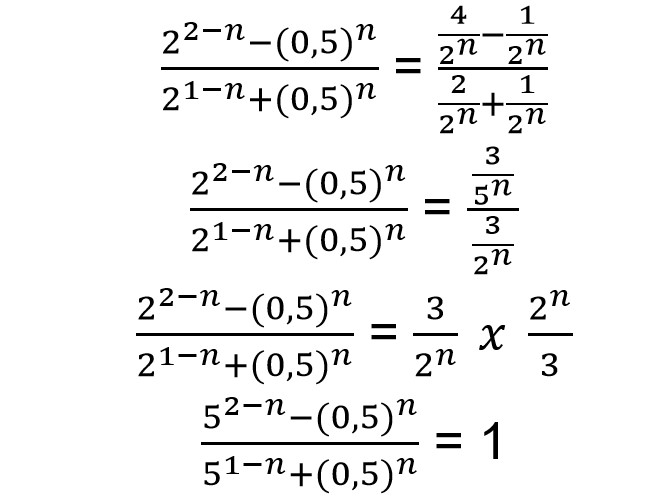
2. Berapakah hasil dari bentuk pangkat berikut
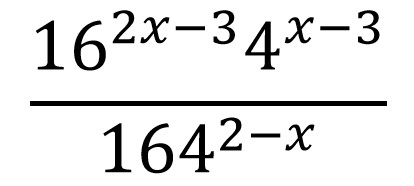
Untuk mengerjakan soal di atas, kamu harus mengingat salah satu sifat operasi dari bilangan yang memiliki pangkat seperti di bawah ini. Kamu bisa menyederhanakan bentuk di atas menggunakan rumus di bawah ini.
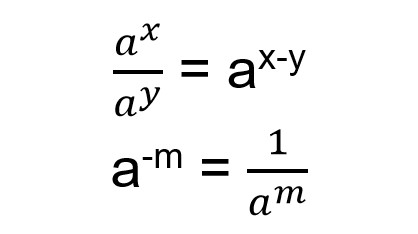
Sehingga cara pengerjaan soal di atas seperti di bawah ini.
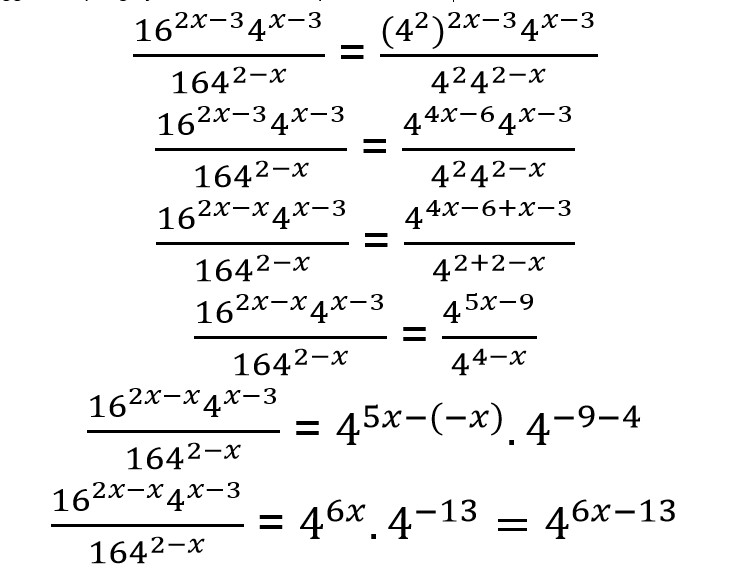
3. Tuliskan bentuk sederhana dari
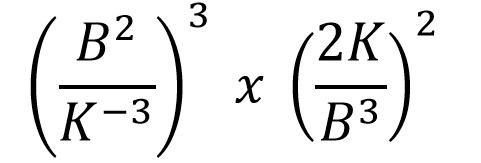
Untuk mengerjakan soal di atas kamu bisa melakukan perkalian pangkat terlebih dahulu seperti di bawah ini.
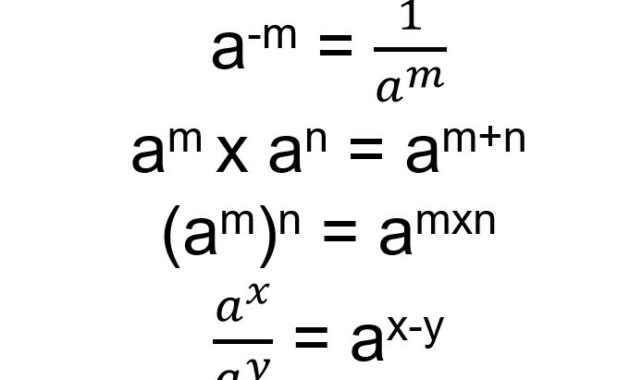
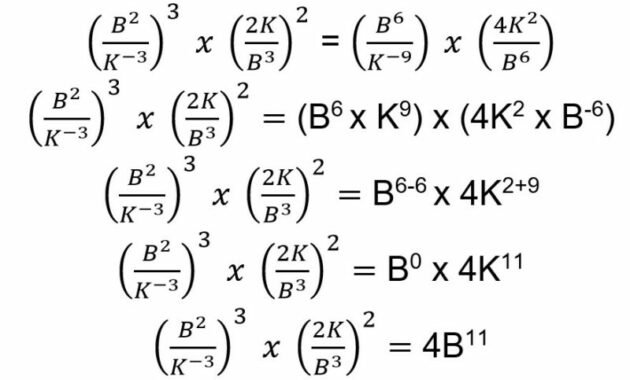
4. Tentukan hasil perhitungan di bawah ini
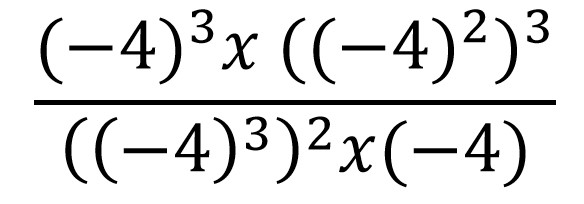
Untuk mengerjakan soal ini, kamu bisa menyederhanakan persamaan di atas sesuai dengan sifat bilangan yang berpangkat.
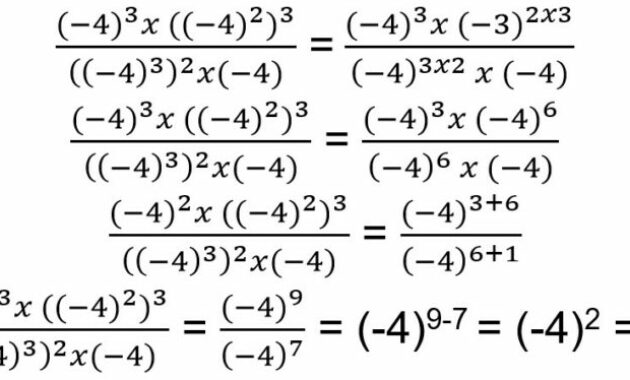
5. Berapakah hasil perkalian 3a5 x 22a2 + 6a5
Untuk mengerjakan soal di atas, kamu bisa mengerjakan persoalan perkalian terlebih dahulu dengan menggunakan aturan pangkat.
am x an = am+n
3a5 x 22a2 +6a5= 3a5 x 4a2 + 6a5
3a5 x 22a2 + 6a5= (3×4)(a5+2) + 6a5
3a5 x 22a2 + 6a5= 12a7 + 6a5 = 6a5 (2a2 + 1)
6. Berapakah hasil penjumlahan berikut
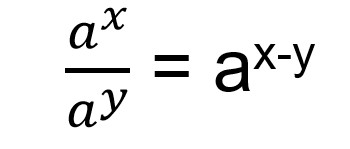
Untuk mengerjakan soal di atas, kamu bisa menggunakan aturan pangkat pembagian.
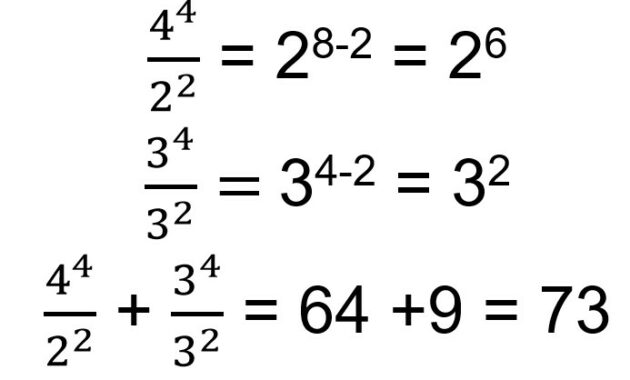
Sehingga kamu bisa mengerjakan soal satu per satu dan kedua hasil pangkat ditambahkan seperti di bawah ini.Belajar bilangan yang memiliki pangkat akan memudahkan kamu dalam menyelesaikan soal-soal yang berhubungan dengan perkalian.
Dengan berlatih soal-soal, kamu akan semakin mudah untuk memahami proses pengerjaan dalam bilangan yang berpangkat beserta dengan operasi hitung yang digunakan.
Baca Juga Lainnya:
